Modellreduktion für mehrere bewegte Fronten mit topologischen Veränderungen
Mitarbeitende
Laufzeit
01.10.2021 - 30.09.2024
Finanzierung
DFG - Projekt-Nummer 384950143 (als Teil des GRK2433 DAEDALUS Projekt Q09)
 © DFG
© DFG
 © DAEDALUS
© DAEDALUS
Grundlegende Idee
In der Optimierung von Strömungen spielt die Modellreduktion von transportdominierten Systemen eine entscheidende Rolle. Beispiele solcher Strömungen sind Phänomene wie die Bewegung von Flüssigkeiten, Wärmeleitung und chemischer Stofftransport. In zahlreichen Gebieten der Wissenschaft und Industrie, wie zum Beispiel der Luft- und Raumfahrttechnik und dem Automobilbau, ist die Optimierung solcher Strömungen von großer Bedeutung. Die Reduktion der Modelle erleichtert dabei die Identifikation von optimalen Mustern in der Strömung, was schnelles Prototyping und Testen von Designs ermöglicht. Außerdem helfen diese Modelle bei der Entwicklung von effizienten Regelungsstrategien zur Anpassung und Optimierung von Strömungen in Echtzeit.
Allerdings birgt die Optimierung von komplexen Strömungen wie konvektionsdominanten Problemen mit bewegten Fronten (beispielsweise Schockwellen oder Flammen) erhebliche Schwierigkeiten, da die zugrundeliegenden Dynamiken nichtlinear sind und daher für die numerische Lösung rechenintensive Simulationen mit einer hohen Zahl an Freiheitsgraden nötig sind. Das Hauptziel unseres Projektes ist die Entwicklung entsprechender Techniken zur Modellreduktion, mit deren Hilfe komplexe Systeme mit geringerem Rechenaufwand simuliert werden können, ohne dabei die Genauigkeit der Modelle aufzugeben.
Ein Beispiel eines solchen Prozesses ist das Modell der Flamme eines Bunsenbrenners. Klassische projektionsbasierte Methoden reduzieren die Dimension des Modells, indem sie einen niedrigdimensionalen Testraum erzeugen auf den die Dynamik des Systems projeziert wird. Allerdings stellt sich heraus, dass der Testraum für diese Art von Problem in der Praxis eine hohe Dimension hat. In den vergangenen Jahren wurden einige Methoden zur Umgehung dieses Problems vorgeschlagen. Eine der moderneren Methoden ist die "shifted proper orthogonal decomposition" (sPOD). Hier wird das hochrangige Lösungsfeld in mehrere Felder mit niedrigem Rang zerlegt, die voneinander abhängen. Diese können dann entweder mit herkömmlichen Methoden der Modellreduktion bearbeitet werden oder man geht über zu rein datengestützten Methoden des machine learning, um die Lösungen vorherzusagen.
Mathematische Formulierung und angewandte Methoden
Es wurden bereits einige Versuche unternommen die Schwierigkeiten in den Methoden der Modellreduktion für transportdominierte Probleme zu bewältigen. In [7, 9] werden parameterabhängige Transformationen der Snapshots vorgeschlagen, die dabei helfen sollen die räumlichen Bewegungen der Fronten anzugleichen. Um den parameterabhängigen Transport auszugleichen wird in [5] eine Methode des machine learning basierend auf convolutionalen Autoencodern verwendet. Diese Methoden haben zwar vielversprechende Ergebnisse geliefert, allerdings wurden sie nur auf standardisierte Probleme wie Advektionsgleichungen und Burgers Gleichung angewendet und für solche getestet. Die sPOD-Methode wurde in [7] vorgeschlagen und in [8, 4] wurden weiterführende Ergebnisse zur Entwicklung von Algorithmen auf der Grundlage der Optimierung von Singulärwerten präsentiert. Die sPOD-Methode versucht die Snapshot-Matrix Q in mehrere voneinander abhängige Felder zu zerlgen, siehe (1).

Die diskreten Transformationsoperatoren basieren auf Interpolation und sind abhängig von den Verschiebungen. Zu sehen sind sie in (2), wo der Zustand q von der Raumvariablen x, der Zeit t und einigen weiteren Parametern abhängt.
Bevor der sPOD-Algorithmus verwendet werden kann, müssen zunächst die Verschiebungen bestimmt werden, die später zur Konstruktion dieser Transformationsoperatoren benötigt werden. Sobald die Snapshot-Matrix erfolgreich zerlegt wurde, werden die Zeitamplituden aus den einzelnen Feldern extrahiert. Dazu werden Basisvektoren verwendet, deren Konstruktion in (3) zu sehen ist.
Mit diesem Ansatz werden die zeit-dynamischen Modelle mit Hilfe von Petrov-Galerkin und Galerkin Methoden [10] konstruiert. Solche Methoden projezieren die ursprüngliche Dynamik auf einen niedrigdimensionalen Unterraum und erzeugen so ein reduziertes System mit wenigen Variablen. Im Gegensatz dazu haben wir uns dazu entschieden für unsere Analyse eine rein datengestützte Methode zu verwenden, der künstliche neuronale Netze zu Grunde liegen. Dabei ist unser Vorgehen inspiriert durch [3]. Wir setzen ein tiefes neuronales Netz ein, das mit den erhaltenen Zeitamplituden und den bekannten Parametern trainiert wird. Nach Abschluss der Lernphase sagt das Netzwerk die Zeitamplituden aller versteckten Parameter voraus. Dadurch kann der Endzustand durch Projektion der Zeitamplituden auf den Testraum, der von sPOD generiert wurde, rekonstruiert werden, siehe (4).
Erzielte Ergebnisse und weiterführende Arbeit
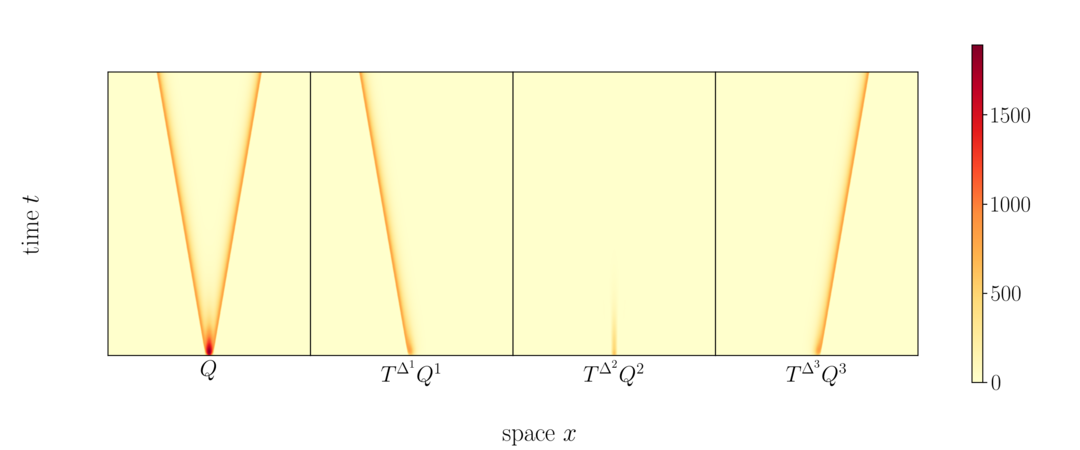
Wir haben unsere Methodik an dem praktisch relevanten Problem von Waldbränden getestet [6]. Die Variablen die wir betrachten sind dabei die Temparatur(T) und die brennbare Masse(S). Zur Konstruktion nichtlinearer parametrisierter reduzierter Modelle lösen wir die Waldbrand-Gleichungen und konstruieren eine parametrisierte Snapshot-Matrix Q. Sobald Q erstellt ist, setzen wir sPOD ein um die Dimension zu reduzieren und erhalten wie oben beschrieben eine niedrigdimensionale Darstellung der Daten. Eine Visualisierung der sPOD-Zerlegung ist in Abbildung 1 zu finden. Die Verschiebungen für die einzelnen Felder, die zur Anwendung von sPOD benötigt werden, werden durch Tracking der Gradienten der Variablen wie in [1] bestimmt. Als Ergebnis der Dimensionsreduktion erhalten wir die Zeitamplitude.
 © S. Burela
© S. Burela
Abbildung 1: Zerlegung vom Temperatur-Feld durch sPOD. Die zweite, dritte und vierte Abbildung zeigen die voneinander abhängigen Felder in die das ursprüngliche Feld zerlegt wurde .
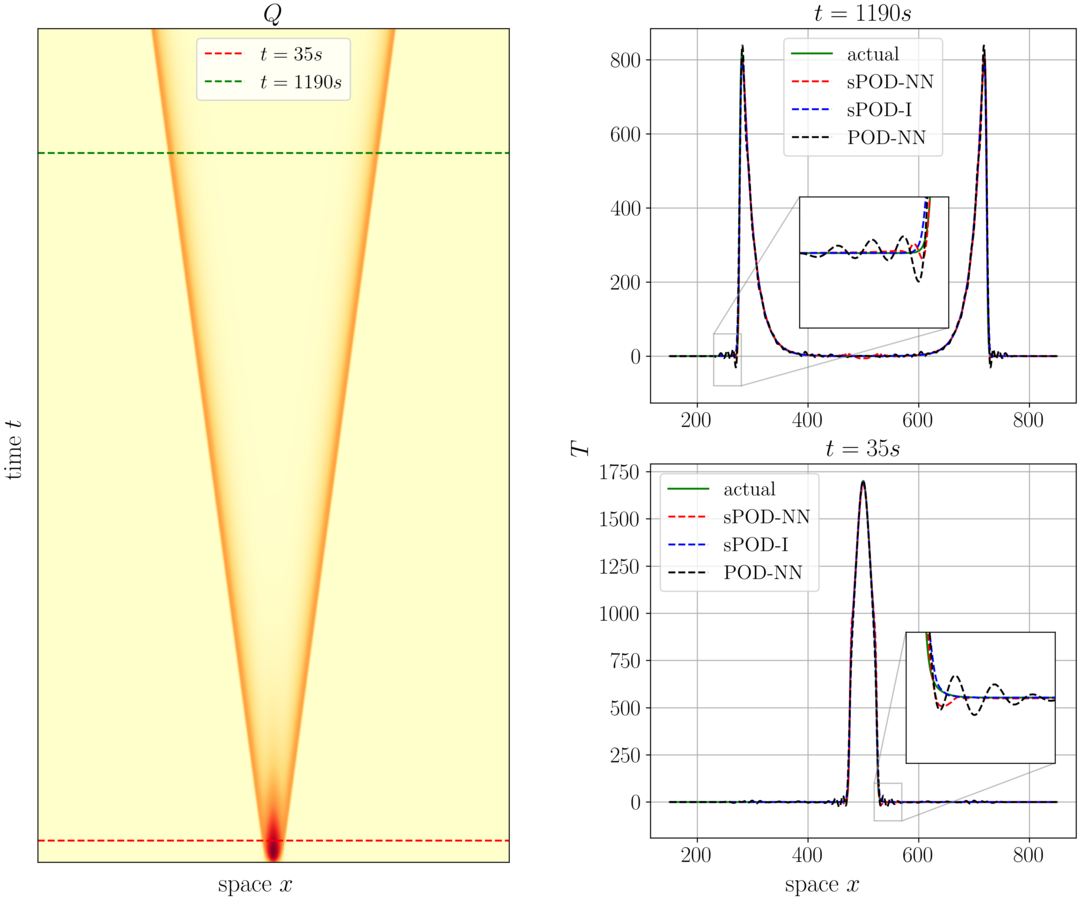
Unser neuronales Netz wird trainiert wie in [2] beschrieben. Um das Netz zu testen verwenden wir es zur Vorhersage der Zeitamplituden und Verschiebungen und rekonstruieren die Lösung wie in Abbildung 2 zu sehen ist. Dort sieht man, dass das sPOD-NN bessere Ergebnisse erzielt als die POD-NN-Methode. Wir haben die sPOD-NN-Methode außerdem an einer zweidimensionalen Erweiterung des Waldbrand-Modells getestet und die Ergebnisse passen zu dem, was wir im eindimensionalen Fall beobachtet haben. Alle weiteren gründlichen Untersuchungen die wir durchgeführt haben können in [2] gefunden werden.
Im Wesentlichen ist es uns gelungen eine rein datenbasierte Modellreduktions-Methode zu entwickeln, wobei wir sPOD als Rekonstruktionsmethode verwenden und wir konnten zeigen, dass diese Technik genauer ist als die POD-NN-Methode. Nun wollen wir uns Methoden zuwenden, die sich nicht nur auf Daten stützen sondern zusätzlich Systeminformationen in Betracht ziehen um transportdominierte Probleme dieser Art zu lösen. Außerdem planen wir diese Methoden für geregelte Systeme zu betrachten, um schlussendlich unser ursprüngliches Ziel der optimalen Regelung transportdominierter Strömungen zu erreichen.
 © S. Burela
© S. Burela
Abbildung 2: Diese Abbildung zeigt die Vorhersagegenauigkeit der untersuchten Methoden. Wir betrachten Querschnitte des Temperaturprofils in den Zeitpunkten t = 35s und 1190s.
Publikationen
[2] Shubhaditya Burela, Philipp Krah, and Julius Reiss. “Parametric model order reduction for a wildland fire model via the shifted POD based deep learning method”. en. In: arXiv (2023). doi: https://doi.org/10.48550/arXiv.2304.14872
Referenzen
[1] Felix Black, Philipp Schulze, and Benjamin Unger. “Efficient Wildland Fire Simulation via Nonlinear Model Order Reduction”. In: Fluids 6.8 (2021), p. 280.
[3] Stefania Fresca and Andrea Manzoni. “POD-DL-ROM: Enhancing deep learning-based reduced order models for nonlinear parametrized PDEs by proper orthogonal decomposition”. In: Computer Methods in Applied Mechanics and Engineering 388 (Jan. 2022), p. 114181.
[4] Philipp Louis Krah. “Non-linear reduced order modeling for transport dominated fluid systems [Doctoral dissertation]”. en. In: (2023).
[5] Kookjin Lee and Kevin Carlberg. Model reduction of dynamical systems on nonlinear manifolds using deep convolutional autoencoders. 2018.
[6] Jan Mandel et al. “A wildland fire model with data assimilation”. In: Mathematics and Computers in Simulation 79.3 (2008), pp. 584–606.
[7] J. Reiss et al. “The Shifted Proper Orthogonal Decomposition: A Mode Decomposition for Multiple Transport Phenomena”. In: SIAM Journal on Scientific Computing 40.3 (2018), A1322–A1344.
[8] Julius Reiss. “Optimization-Based Modal Decomposition for Systems with Multiple Transports”. In: SIAM Journal on Scientific Computing 43.3 (2021), A2079–A2101.
[9] Donsub Rim, Scott Moe, and Randall J. LeVeque. “Transport Reversal for Model Reduction of Hyperbolic Partial Differential Equations”. In: SIAM/ASA Journal on Uncertainty Quantification 6.1 (2018), pp. 118–150.
[10] Clarence W. Rowley, Tim Colonius, and Richard M. Murray. “Model reduction for compressible flows using POD and Galerkin projection”. In: Physica D: Nonlinear Phenomena 189.1 (2004), pp. 115–129.
